glTF-Tutorials
| Previous: Simple Meshes | Table of Contents | Next: Materials |
Meshes
The Simple Meshes example from the previous section showed a basic example of a mesh with a mesh.primitive object that contained several attributes. This section will explain the meaning and usage of mesh primitives, how meshes may be attached to nodes of the scene graph, and how they can be rendered with different materials.
Mesh primitives
Each mesh contains an array of mesh.primitive objects. These mesh primitive objects are smaller parts or building blocks of a larger object. A mesh primitive summarizes all information about how the respective part of the object will be rendered.
Mesh primitive attributes
A mesh primitive defines the geometry data of the object using its attributes dictionary. This geometry data is given by references to accessor objects that contain the data of vertex attributes. The details of the accessor concept are explained in the Buffers, BufferViews, and Accessors section.
In the given example, there are two entries in the attributes dictionary. The entries refer to the positionsAccessor and the normalsAccessor:
"meshes" : [
{
"primitives" : [ {
"attributes" : {
"POSITION" : 1,
"NORMAL" : 2
},
"indices" : 0
} ]
}
],
Together, the elements of these accessors define the attributes that belong to the individual vertices, as shown in Image 9a.
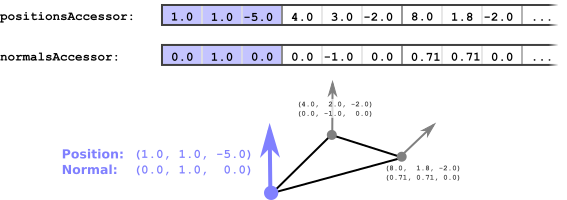
Image 9a: Mesh primitive accessors containing the data of vertices.
Indexed and non-indexed geometry
The geometry data of a mesh.primitive may be either indexed geometry or geometry without indices. In the given example, the mesh.primitive contains indexed geometry. This is indicated by the indices property, which refers to the accessor with index 0, defining the data for the indices. For non-indexed geometry, this property is omitted.
Mesh primitive mode
By default, the geometry data is assumed to describe a triangle mesh. For the case of indexed geometry, this means that three consecutive elements of the indices accessor are assumed to contain the indices of a single triangle. For non-indexed geometry, three elements of the vertex attribute accessors are assumed to contain the attributes of the three vertices of a triangle.
Other rendering modes are possible: the geometry data may also describe individual points, lines, or triangle strips. This is indicated by the mode that may be stored in the mesh primitive. Its value is a constant that indicates how the geometry data has to be interpreted. The mode may, for example, be 0 when the geometry consists of points, or 4 when it consists of triangles. These constants correspond to the GL constants POINTS or TRIANGLES, respectively. See the primitive.mode specification for a list of available modes.
Mesh primitive material
The mesh primitive may also refer to the material that should be used for rendering, using the index of this material. In the given example, no material is defined, causing the objects to be rendered with a default material that just defines the objects to have a uniform 50% gray color. A detailed explanation of materials and the related concepts will be given in the Materials section.
Meshes attached to nodes
In the example from the Simple Meshes section, there is a single scene, which contains two nodes, and both nodes refer to the same mesh instance, which has the index 0:
"scenes" : [
{
"nodes" : [ 0, 1]
}
],
"nodes" : [
{
"mesh" : 0
},
{
"mesh" : 0,
"translation" : [ 1.0, 0.0, 0.0 ]
}
],
"meshes" : [
{ ... }
],
The second node has a translation property. As shown in the Scenes and Nodes section, this will be used to compute the local transform matrix of this node. In this case, the matrix will cause a translation of 1.0 along the x-axis. The product of all local transforms of the nodes will yield the global transform. And all elements that are attached to the nodes will be rendered with this global transform.
So in this example, the mesh will be rendered twice because it is attached to two nodes: once with the global transform of the first node, which is the identity transform, and once with the global transform of the second node, which is a translation of 1.0 along the x-axis.
| Previous: Simple Meshes | Table of Contents | Next: Materials |